Machine Learning for Quantum Physics
Exploring Artificial Intelligence for Many Body Quantum Systems
Artificial intelligence and quantum materials are now revolutionizing the way we relate to the world. The first, in its machine learning and deep learning facets, is now present in every aspect of our lives, from smartphones to automation in our homes. Quantum materials, obeying the bizarre rules of quantum mechanics, promise instead to play a fundamental role in the field of new technologies and sustainable energies.
However, it is not easy to imagine a meeting point between these two revolutionary spheres. Nevertheless, more and more often in recent years, artificial intelligence and the quantum description of the world around us have intersected, thus giving rise to new methods for studying the microscopic behavior of matter.
Phenomena and properties such as magnetism and superconductivity owe their origin to the way elementary particles, electrons, interact with each other. The description of these interactions, and the phenomenologies that emerge from them, have occupied the minds of the best physicists for more than a century. Many theoretical models have thus been developed, but none of them has so far been able to give a definite answer to the “many electron problem”.
Deep Learning the Functional Renormalization Group
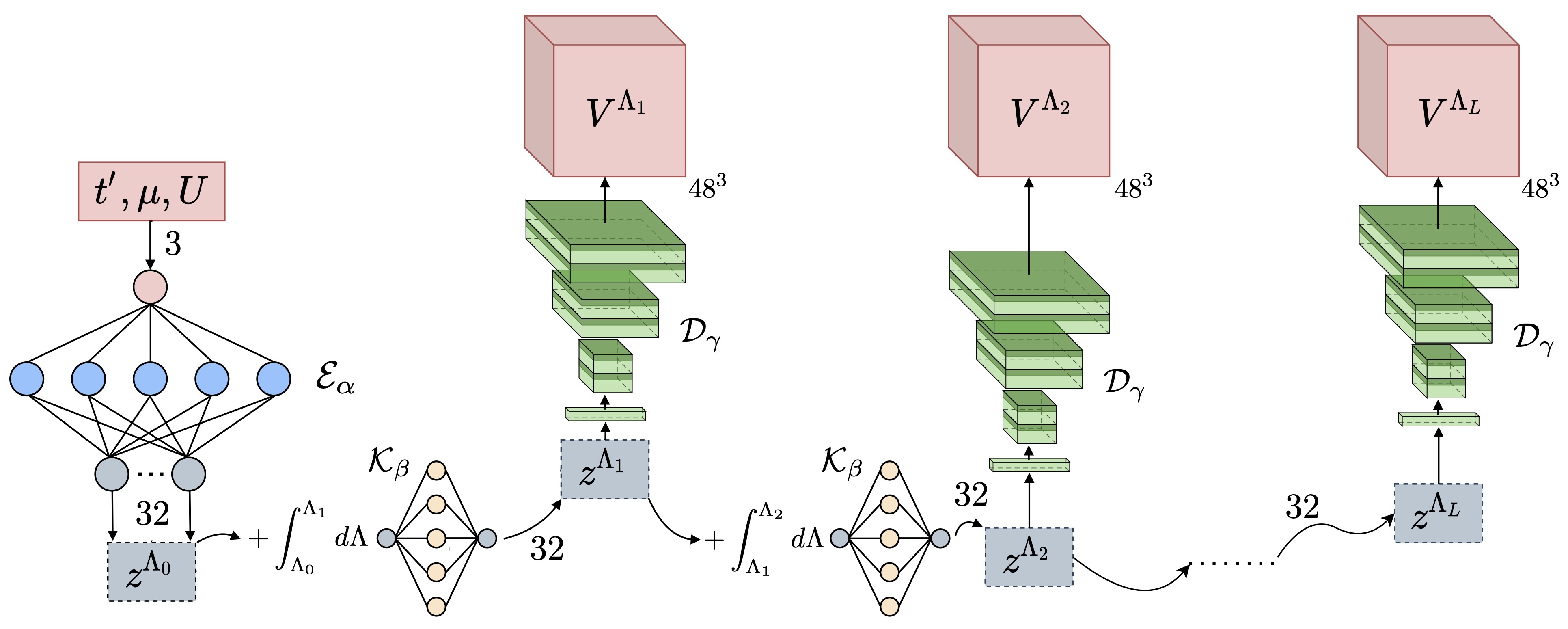
One of the most versatile of these methods is the so-called functional renormalization group, which was born on the basis of that fundamental theoretical construction that is the renormalization group, for which Kenneth G. Wilson won the Nobel Prize for physics in 1982. A little more in detail, the way in which electrons “communicate” with each other is formalized through a very large number of so-called coupled differential equations, up to tens of millions. The latter form the essential mathematical language of the physical interpretation of all natural phenomena, from the movement of celestial stars, to weather forecasts, right up to the quantum behavior of elementary particles.
Our research work has shown, for the first time, how these differential equations can be efficiently described, and above all simplified, through suitable neural networks that form the basis of the so-called deep learning. Hence the title of the publication Deep learning the functional renormalization group. Furthermore, since the functional renormalization group provides a temporal dynamics in the so-called renormalization time, which in our case is the temperature of the interacting electron system, the problem has also been analyzed in the context of Koopman’s spectral theory, which in the last decade it has emerged as the dominant perspective in the study of non-linear dynamical systems.
The work is the result of the Marie Curie BITMAP research project, funded by the European community under the Horizon 2020 initiative, of which the University of Bologna is a beneficiary through the Department of Physics.
The work was carried out mainly in New York, at the prestigious Center for Computational Quantum Physics of the Flatiron Institute of the Simons Foundations, during the so-called outgoing phase of the project. The main purpose of the BITMAP project is precisely to explore possible applications of artificial intelligence and machine learning in the context of describing the interaction between electrons in quantum materials.
Divulgation and outreach:
Artificial Intelligence Reduces a 100,000-Equation Quantum Physics Problem to Only Four Equations
Fisica quantistica: da 100.000 a quattro equazioni, grazie all’intelligenza artificiale
